Inicial > arXiv, hep-th, math-ph, Mathematics, Physics, Science > Fluxo de Ricci, Flutuações Quânticas e Geometria…

Fluxo de Ricci, Flutuações Quânticas e Geometria…

quarta-feira, 18 fev 2009; \08\America/New_York\America/New_York\k 08 Deixe um comentário Go to comments

Já faz algum tempo que eu quero escrever sobre esse assunto: flutuações quânticas, fluxo de Ricci, geometria, fluxo do grupo de renormalização e afins. Agora parece ser o momento certo… 😉

De saída, digo que todas as estruturas matemáticas ou físicas possuem as propriedades necessárias pros resultados citados valerem, FAPP. Assim, isso economiza uma série de “observações” que deveriam ser feitas… mas, facilita um tanto a visão geral e o objetivo das construções feitas.

Introdução

Vamos começar definindo um básico de notação: \Sigma e \mathscr{M} são variedades Riemannianas e \phi:\; \Sigma\longrightarrow\mathscr{M} são mapas/funções parametrizadas por um conjunto de constantes de acoplamentos \mathcal{C}; os espaços \mbox{Map}(\Sigma,\mathscr{M}) = \{ \phi \; : \; \Sigma\longrightarrow\mathscr{M}\} têm um significado matemático “razoável”, onde não assumimos nenhuma propriedade de regularidade (forte) sobre os mapas \phi; e, por definição, \mbox{dim}(\Sigma) é a dimensão da QFT dada. Vale a pena, ainda por cima, pensarmos em termos dum espaço [formal] \mbox{Act}[\mbox{Map}(\Sigma,\mathscr{M})\times \mathcal{C}], onde cada ponto representa um funcional em \mbox{Map}(\Sigma,\mathscr{M})\times\mathcal{C}, chamado de Ação, S[\phi;\alpha], onde (\phi,\alpha) \in \mbox{Map}(\Sigma,\mathscr{M})\times\mathcal{C} e S[\phi;\alpha] \in\mathbb{R}. Na verdade, uma QFT é associada naturalmente a uma órbita da Ação clássica S[\phi;\alpha], gerada em \mbox{Act}[\mbox{Map}(\Sigma,\mathscr{M})\times \mathcal{C}] por um semi-grupo cuja existência dá um significado físico apropriado ao processo de quantização.

Vamos agora nos lembar que uma QFT (Euclidiana) é totalmente determinada por suas Funções de Green, i.e., pelas correlações induzidas por uma família de densidade de probabilidades (i.e., medidas) em \mbox{Map}(\Sigma,\mathscr{M}) também parametrizadas por \mathcal{C}, entre os valores \phi(x_1,\dotsc, x_k) \in \mathscr{M}^k, onde (x_1,\dotsc, x_k)\in\Sigma:

Z[\phi(x_k);\alpha] \equiv \displaystyle\int_{\mbox{Map}(\Sigma,\mathscr{M})} \phi(x_1,\dotsc,x_k)\, e^{-S[\phi;\alpha]}\, D_{\alpha}[\phi] \; ;

onde D_{\alpha}[\phi] is a functional measure in \mbox{Map}(\Sigma,\mathscr{M}).

Dando uma interpretação geométrica ao cenário acima, mesmo no caso 0-dimensional nós já temos resultados não-triviais, onde \Sigma = p e \phi:\, p\longrightarrow \mathscr{M} tal que p\mapsto \phi(p) e \mbox{Map}(\Sigma,\mathscr{M}) = \{\phi:\, p\longrightarrow \mathscr{M} \} \simeq \mathscr{M}. Nesse caso, o funcional Ação se torna uma função escalar (para o caso em questão, nos reais) e usando-se o método de “steepest descent” (ou “stationary phase”) a Função de Partição desse problema (que se reduz a uma integral) se localiza (i.e., tem suas maiores contribuições) nos pontos críticos da Ação — notem que esses pontos críticos variam de acordo com os acoplamentos \alpha sendo considerados; variando-se esses acoplamentos obtém-se toda sorte de fenômeno no espaço de parâmetros \mathcal{C}, como Stokes Phenomena e Lee-Yang Zeros (vejam também Statistical Theory of Equations of State and Phase Transitions. I. Theory of Condensation e Statistical Theory of Equations of State and Phase Transitions. II. Lattice Gas and Ising Model) que acabam gerando fenômenos de catástrofe no espaço de parâmetros \mathcal{C} o que leva à quebra espontânea de simetria e transição de fases. (Mas, quero deixar pra comentar sobre isso mais tarde, pois as ligações com o fluxo de Ricci e do Grupo de Renormalizacão vão ser bem bonitas. 😉 )

Agora um “truque” que eu praticamente não vejo sendo usado: ao invés de se usar \phi\in\mathbb{R}, é bom sempre ter em mente que é possível se usar outros tipos de campos, como \phi\in\mathbb{R}^{n\times n} ou \phi\in\mathfrak{su}(N) — ou seja, seguindo a linha de raciocínio que estamos traçando aqui, basta escolhermos \mathscr{M} de modo apropriado, i.e., ou sendo o espaço de matrizes [Hermitianas] n\times n ou sendo uma variedade do grupo de Lie \mbox{SU}(N). Dessa forma, é praticamente uma extensão trivial se obter os resultados análogos para campos matriciais ou com valores em álgebras de Lie. (Esse caminho nos leva a considerações do tipo Intersection theory on the moduli space of curves and the matrix Airy function, e suas extensões em Airy Functions for Compact Lie Groups. Isso mostra que as Funções de Partição podem ser vistas, genericamente, como Funções de Airy generalizadas e, aí, se pode aplicar todo um maquinário de “intersection theory on moduli spaces” para se encontrar todas as possíveis soluções duma determinada QFT… aliás, é assim que se aplica QFT para se classificar variedades. 😉 ) Ou seja, se fizermos \mathscr{M} = \mathcal{H}^{n\times n}, o espaço de matrizes hermitianas n\times n, é possível estudarmos toda uma série de problemas em geometria enumerativa, estabelecendo uma conexão profunda entre QFTs 0-dimensionais e a topologia do ‘moduli space’ de superfícies de Riemann! E, como vcs já podem ter percebido, as diferentes soluções que aparecem nesses problemas de geometria enumerativa e de Teoria da Intersecção estão intimamente ligadas às fases (i.e., quebra espontânea de simetria) que uma determinada QFT tem. Mas, essas ligações são complicadas de serem estabelecidas e não me parece haver literatura a respeito disso (até a publicação da minha tese, 😈 ).

Falando em termos de 1-dim QFTs, temos explicitamente a Mecânica Quântica, que não passa de \Sigma = \mathbb{R} para uma linha (tempo) ou \Sigma = S^{1} para MQ num círculo (tempo Euclidiano ou temperatura). Nesse caso, a Função de Partição descreve um processo de Wiener em \mathscr{M} (também conhecido como Movimento Browniano). Dessa forma, como estamos falando de espaços Euclidianos, percebemos que a MQ não passa duma rotação de Wick dum processo de Wiener — pra quem gosta dessa visão (que é menos simples do que parece, claro 😉 ), eu recomendo a leitura do livro Quantum Fluctuations do Nelson.

Geometricamente falando, pode se dizer que no caso de QFT 1-dim (Euclidiana), a Função de Partição “sente” como as flutuações [quânticas] afetam os caminhos aleatórios t\mapsto \phi(t)\in\mathscr{M}, conforme variamos a escala de “comprimentos” \Delta t em \Sigma — dessa forma, estamos lidando com a quantização do fluxo geodésico em \mathscr{M} e podemos fazer a identificação “Geometria Riemanniana de \mathscr{M}” \Longleftrightarrow “MQ de partículas teste em \mathscr{M}“! 😎 (Aposto como agora fica mais fácil de se entender a importância da Métrica de Jacobi, usada em arXiv:0809.2778, para transformar um fluxo Hamiltoniano num fluxo geodésico. 😈 )

O Fluxo do Grupo de Renormalização

Os exemplos acima lidam com situações onde as flutuações quânticas podem ser usadas pra medir diferentes aspectos da geometria de (\Sigma,\mathscr{M}), porém, sem afetá-la diretamente. Portanto, a partir de agora, podemos começar a nos perguntar ‘se’ e ‘quanto’ as flutuações quânticas de \phi:\, \Sigma\rightarrow\mathscr{M} podem deformar a geometria do par (\Sigma,\mathscr{M}).

Para atacar tal pergunta, é necessário “controlarmos” tanto os campos, \phi:\, \Sigma\rightarrow\mathscr{M}, quanto as constantes de acoplamento, \alpha\in\mathcal{C}, na medida em que variamos as escalas em \Sigma (que é a única escala significativa numa teoria [quântica] relativística. :wink:)

Ou seja, é preciso reconhecermos duma vez por todas — e logo de saída! 😛 — que um dos ingredientes básicos de qualquer QFT é uma escala de energias. Há vários modos diferentes de se ver isso; e.g., em termos de Wilson Loops, isso está relacionado ao tamanho da curva C que dá sentido à path-ordered exponential (i.e., está relacionado à localidade da holonomia sendo usada); na formulação da QFT em redes (ou seja, em Mecânica Estatística 😉 ), isso tem a ver com as variáveis de bloco escolhidas pra teoria (i.e., com o tamanho dos blocos); falando em termos de OPEs, significa escolher a álgebra de operadores de vértice (VOA) que codifica o comportamento da teoria numa dada escala de energia (i.e., ela codifica as propriedades importantes dum particular complemento ultra-violeta); e, finalmente, alguém pode gritar, lá do fundão: “Grupo de Renormalização”. 🙂 Ou seja, determinar as holonomias da teoria, ou as variáveis de bloco ou o [particular] fluxo do grupo de renormalização (que se deseja tratar no caso em mãos), é tudo a mesma coisa. 😉

Ou seja, é fundamental procurarmos por um conjunto de transformações (fluxo do grupo de renormalização) tais que,

\mbox{RG}_{\ell}\, : \; \mbox{Map}(\Sigma, \mathscr{M})\times\mathcal{C} \longrightarrow \mbox{Map}(\Sigma, \mathscr{M})\times\mathcal{C}

\therefore\qquad\qquad\qquad\;\, (\phi,\alpha) \longmapsto \mbox{RG}_{\ell}(\phi,\alpha) = \bigl(\phi_{\ell};\alpha(\ell)\bigr) \; .

Assim, quando variamos a escala \ell em que medimos a superfície de Riemann \Sigma, podemos domar a energia das flutuações dos campos, ajustando as constantes de acoplamento de acordo. (Só pra constar, vou usar \ell = \Lambda^{-1}, onde \Lambda é a escala de momentos no espectro das flutuações dos campos. Então, quando eu quiser ser mais específico sobre as escalas de energias, eu vou usar \Lambda, caso contrário, usarei \ell.)

Portanto, se temos duas escalas, \Lambda, \, \Lambda', e queremos descobrir o que acontece quando \Lambda\rightarrow\Lambda' (i.e., quando fluímos a teoria duma escala para outra), basta realizarmos a seguinte operação:

S'[\phi';\alpha'] = \mbox{RG}_{\Lambda\rightarrow\Lambda'} S[\phi;\alpha] \; .

Essa é a essência das Teorias Efetivas (ver também Grupo de Renormalização).

Porém, pra que essa construção seja possível, é preciso que o mapa \mbox{RG} satisfaça a propriedade de semi-grupo:

\mbox{RG}_{\Lambda\rightarrow\Lambda''} = \mbox{RG}_{\Lambda\rightarrow\Lambda'} \circ \mbox{RG}_{\Lambda'\rightarrow\Lambda''} \; ; \; \forall\; \Lambda > \Lambda' > \Lambda'' \; ;

ou seja, é possível se fluir um sistema (no sentido do grupo de renormalização) apenas na direção de altas energias (resp. pequenas distâncias) para baixas energias (resp. grandes distâncias).

Falando em termos geométricos, uma QFT é caracterizada por uma ação S[\phi;\alpha] somente se a medida funcional a ela associada — e^{-S[\phi;\alpha]}\, D_{\alpha}[\phi] — se transformar “naturalmente” sob \mbox{RG}:

\displaystyle\int_{\mbox{RG}_{\ell}\{\mbox{Map}(\Sigma,\mathscr{M})\}} \exp\{-S[\phi;\alpha]\}\, D_{\alpha}[\phi] = \displaystyle\int_{\mbox{Map}(\Sigma,\mathscr{M})} \exp\{-\mbox{RG}_{\ell}^{*}(S[\phi;\alpha])\}\, \mbox{RG}_{\ell}^{*}\bigl(D_{\alpha}[\phi]\bigr) \; ;

de forma que essa igualdade seja válida no limite \ell\rightarrow 0 (resp. \Lambda\rightarrow\infty).

É importante, porém, sempre se lembrar que \mbox{RG}_{\ell}, apesar do nome, é apenas um semifluxo: com o passar do tempo (i.e., para t\rightarrow +\infty), nós descrevemos um espectro de flutuações de campos para distâncias cada vez maiores, “averaging and integrating out” graus-de-liberdade irrelevantes. Portanto, a validade da fórmula acima no limite t\rightarrow -\infty (resp. \ell\rightarrow0 e \Lambda\rightarrow\infty) é algo altamente não-trivial, uma vez que é muito difícil (quiçá impossível) reverter esse processo (i.e., ir na direção de altas energias e pequenas distâncias). É por essa razão que QFTs são conceitualmente difíceis de serem construídas. 😉

De qualquer maneira, quando é possível se fazer tal construção, a equação acima diz que existe um espaço limite, \lim_{\Lambda\rightarrow\infty} \mbox{RG}_{\Lambda}\{\mbox{Map}(\Sigma, \mathscr{M})\} (i.e., o limite de altas energias dos campos, também chamado de “complemento ultra-violeta” 😉 ), de objetos geométricos que descrevem a QFT em mãos — tipicamente, esses objetos não pertencem ao espaço original, \mbox{Map}(\Sigma, \mathscr{M}) (i.e., os campos iniciais não são os mesmos que os finais, depois que se aplicou um determinado fluxo do grupo de renormalização — os campos renormalizados não são os mesmos que os campos não-renormalizados 😛 ), uma vez que o fluxo de \mbox{RG}_{\Lambda} pode ser altamente singular.

Para discutir esse tipo de questão, vamos tomar a Função de Partição como sendo,

Z[\phi_{\Lambda}; \alpha(\Lambda)] \equiv \displaystyle\int_{\mbox{Map}(\Sigma, \mathscr{M})} \exp\bigl\{-\mbox{RG}_{\Lambda}^{*}(S[\phi;\alpha])\bigr\}\, \mbox{RG}_{\Lambda}^{*}\bigl(D_{\alpha}[\phi]\bigr) \; ;

e reescrever a relação anterior em sua forma diferencial,

\displaystyle\frac{d}{d\Lambda} Z[\phi_{\Lambda}; \alpha(\Lambda)] = \biggl\{\displaystyle\frac{\partial}{\partial\Lambda} - \beta(\alpha(\Lambda))\, \displaystyle\frac{\partial}{\partial \alpha}\biggr\}\, Z[\phi_{\Lambda}; \alpha(\Lambda)] = 0 \; ;

onde \beta(\alpha(\Lambda)) \equiv -\partial\alpha(\Lambda)/\partial\Lambda, é a chamada “função β” da teoria. 😉

Como vcs vêm, a função β pode ser considerada como um campo vetorial (linhas de fluxo) no espaço de parâmetros, \mathcal{C}. A grosso modo, o que isso significa é que se nós re-escalarmos as energias em \Sigma por um fator de e^{\Lambda} e ao mesmo tempo fluirmos no espaço de parâmetros na direção de -\beta por uma quantidade de \Lambda, a teoria obtida tem a mesma forma que a inicial. (Nesse sentido, é sempre bom acompanhar uma discussão como essa com um pouco de Análise Dimensional — quiçá até com um pouco de Teorema π de Buckingham 😉 —, principalmente como feito no artigo Dimensional Analysis in field theory, devidamente comentado em Renormalization as Dimensional Analysis.)

O Fluxo de Ricci e Modelos σ Não-Lineares

[N.B.: A grande vantagem em se estudar Modelos σ não-lineares é que eles servem de “caso teste”, de “modelo de brinquedo”, para teorias de gauge, no sentido de que se considerarmos apenas seus temos cinéticos, já temos uma dinâmica extremamente rica; i.e., não é preciso, necessariamente, haver termos de pontecial pra haver uma dinâmica não trivial — no caso dos modelos σ não-lineares, essa dinâmica é dada pela métrica (não-trivial).]

Um modelo σ não-linear é uma QFT 2-dimensional onde \Sigma é uma superfície Riemanniana 2-dimensional com uma métrica \gamma = \gamma_{\mu\, \nu}\, dx^{\mu}\otimes dx^{\nu}, e o espaço alvo, \mathscr{M}, é uma variedade Riemanniana com a métrica g = g_{i\, j}\, d\phi^{i}\otimes d\phi^{j}. Particularmente, vamos assumir que \Sigma = T^2 = \mathbb{R}^2/\mathbb{Z}^2, i.e., o toro plano, com a métrica \gamma_{\mu\, \nu} = \delta_{\mu\, \nu}. Assumindo que os campos sejam diferenciáveis (pelo menos no sentido de distribuições) e que a L^{2}(\Sigma)-norma de d\phi é finita, é possível se definir a Ação clássica dos campos/mapas \phi\,:\; \Sigma\longrightarrow\mathscr{M} da seguinte forma:

S(\phi; a^{-1}\, g) \equiv a^{-1}\, |d\phi|^{2}_{L^{2}(\Sigma)} = a^{-1}\, \displaystyle\int_{\Sigma} \gamma^{\mu\, \nu}\, \partial_{\mu}\phi^{i}\, \partial_{\nu}\phi^{j}\, g_{i\, j}\, d\mu_{\gamma} \; ;

onde d\mu_{\gamma} é o elemento de volume Riemanniano em (\Sigma,\gamma), e a > 0 é um parâmetro com dimensões de comprimento ao quadrado — notem que a métrica a^{-1}\, g(\phi) faz o papel das constantes de acoplamento para os campos da teoria; o que sugere, nesse caso, que o espaço de parâmetros é o cone ∞-dimensional das métricas Riemannianas sobre \mathscr{M}, chamado de \mbox{Met}(\mathscr{M}). Entretanto, como a Ação acima é invariante pelo grupo de difeomorfismos \mbox{Diff}(\mathscr{M}), na verdade temos que \mathcal{C} = \mbox{Met}(\mathscr{M})/(\mbox{Diff}(\mathscr{M})\times\mathbb{R}^{+}), onde \mathbb{R}^{+} denota o grupo de re-escalamentos definido por a\mapsto \lambda\, a\; ;\; \lambda\in\mathbb{R}^{+}. Portanto, \mathcal{C} é o espaço de estruturas Riemannianas em \mathscr{M} módulo re-escalas (globais) de comprimento. Mais ainda, é importante notar que o único parâmetro adimensional da teoria é a razão entre a escala de comprimentos do espaço alvo (i.e., seu raio de curvatura ao quadrado, r^{2}_{\mbox{curvatura}}) e a. Dessa forma, o limite de acoplamentos fracos em teoria de perturbação acontece quando o tamanho da superfície (\Sigma,\gamma) é muito menor que a escala física de comprimentos em (\mathscr{M},g) (também chamado de “limite puntual”). Para entender esse último ponto um pouco mais profundamente, lembre-se que a Ação acima, além de invariante pelo grupo de difeomorfismos, também é invariante por transformações conformes de (\Sigma,\gamma). Seus pontos críticos são funções harmônicas; em particular, os mínimos são funções constantes. Isso implica que, quando a curvatura do espaço alvo (\mathscr{M},g) for pequena em relação à (\Sigma,\gamma) (i.e., no “limite puntual”), a medida \exp\{-S[\phi;a^{-1}\, g]\}\, D_{g}[\phi] fica concentrada/localizada ao redor das funções constantes e, então, podemos controlar as flutuações quasi-Gaussianas — com um pouco de abuso de linguagem, tipicamente se chama esse caso de “teoria de perturbação para a pequeno”, e dizer que a teoria é “renormalizável perturbativamente em termos do parâmetro de escala a.” 😉

[N.B.: Há vários outros termos que poderiam ser adicionados à Ação acima ainda preservando a invariância por difeomorfismos (porém, tipicamente quebrando a invariância conforme). Os mais comuns são: táquion, dilaton e topológico. Mas, nós não vamos considerá-los aqui, para o bem da clareza de exposição. 😎 ]

Devemos notar que tipicamente o espaço \mbox{Map}(\Sigma,\mathscr{M}) é não-linear (i.e., não é um espaço vetorial), e é difícil de se implementar o procedimento do grupo de renormalização num cenário desses. Porém, no limite de de acoplamentos fracos (i.e., no “limite puntual” acima), somente campos que flutuam ao redor de valores constantes são relevantes. Dessa forma, a idéia é a de descrever o Modelo σ não-linear em mãos se extraindo o comportamento das flutuações quânticas dos campos \phi ao redor dum ‘background’ \psi (i.e., “campo médio”), definido pela distribuição do centro-de-massa dum grande número (tendendo ao infinito) de cópias independentes de \phi.

Nesse ponto, pra não matar ninguém de tedius-maximus-totalis, 😉 , vou dar um pulinho… e ir direto pra parte que interessa, pro filezinho: o fluxo do grupo de renormalização para um modelo σ não-linear. 😎 Nas referências abaixo vcs podem encontrar os detalhes mais sórdidos. 😉

Então, essencialmente, o fluxo do grupo de renormalização para modelos σ não-lineares, em 1-loop e 2-loops, é, respectivamente, o seguinte:

  • 1-loop: \displaystyle\frac{\partial}{\partial t} g(t) = -2\, \mbox{Ric}\bigl(g(t)\bigr) + \mathcal{O}(a^{2});
  • 2-loops: \displaystyle\frac{\partial}{\partial t} g_{i\, k}(t) = -2\, R_{i\, k}(t) - a\, (R_{i\,l\,m\,n}\, R^{l\,m\,n}_{k}) + \mathcal{O}(a^{2});

onde t = -a\, \log(\Lambda/\Lambda') (de tal forma que \Lambda seja o “cutoff” de momento tal que os \phi com momento menor que \Lambda estejam confinados por campos onde \Lambda' representa o termo de massa necessário para a regularização [desse último]), \mbox{Ric} é o tensor de Ricci e R_{a\,b\,c\,d} é o tensor de curvatura de Riemann.

No “limite puntual” (i.e., acoplamento fraco, a\rightarrow 0), ambas as expressões se tornam o Fluxo de Ricci (de R. Hamilton):

\displaystyle\frac{\partial}{\partial t} g_{a\,b}(t) = -2\, R_{a\,b}(t)\; ,\; g_{a\,b}(0) = g_{a\,b} \; .

Geometricamente, esta é a equação de evolução fracamente-parabólica obtida através da deformação duma métrica Riemanniana, g_{a\,b}, sobre a variedade suave \mathscr{M} na direção do tensor de Ricci R_{a\,b} [dessa variedade \mathscr{M}]. É importante notarmos que esse fluxo, essa evolução, só é fracamente-parabólica no regime infra-vermelho do fluxo do grupo de renormalização (correspondendo ao limite t\rightarrow\infty), enquanto que o limite \Lambda/\Lambda' \rightarrow\infty corresponde ao regime parabólico inverso, t\rightarrow -\infty.

Em particular, o modelo σ não-linear é renormalizável (i.e., existe como uma teoria no contínuo) se, e somete se, começando da métrica nua g, nós podemos fazer o fluxo de Ricci para trás no “tempo” até t = -\infty sem encontrar singularidades — i.e., podemos tomar o limite inverso (tempos negativos) do fluxo de Ricci sem encontrar singularidades. Também é importante notar que se a métrica obtida a partir do fluxo de Ricci desenvolver uma região de alta curvatura, então a correspondência entre “fluxo de renormalização” e “fluxo de Ricci” deixa de existir — nesse caso é preciso se considerar, pelo menos, o termo a\, (R_{i\,l\,m\,n}\, R^{l\,m\,n}_{k}), e o comportamento a grandes distâncias (t\rightarrow +\infty) pode depender fortemente de termos topológicos (adicionados à Ação original). Por outro lado, o desenvolvimento de singularidades quando t diminui implica que não podemos remover o ‘curoff’ ultra-violeta \Lambda (i.e., não há um “complemento UV” para a teoria). A Ação não define uma teoria de campos locais, e o melhor que se pode esperar é uma descrição efetiva válida em alguma escala t_0.

[N.B.: A pergunta que fica, agora, é a seguinte, O que representam essas tais ‘singularidades do fluxo de Ricci’? A resposta pra essa pergunta nos leva ao próximo (e último) assunto a ser tratado nesse post… mas, deixo uma diquinha: “transição de fases” e “quebra espontânea de simetria”. 😈 ]

A Geometria do Fluxo de Ricci e Comentários sobre suas Singularidades

O fluxo de Ricci foi o ponto-de-partida e o exemplo motivador em importantes desenvolvimentos em Análise Geométrica, tendo seu ápice na prova da Conjectura da Geometrização de Thurston e da Conjectura de Poincaré! 😯 Então, isso torna ainda mais impressionante o fato de que fluxos de Ricci aparecem tão naturalmente na análise do grupo de renormalização de modelos σ não-lineares.

O fato geométrico que trabalha nos batidores para tornar toda essa mágica possível é que a função $beta; do fluxo do grupo de renormalização poder ser interpretada como sendo um campo vetorial no espaço de parâmetros, \mathcal{C} da QFT dada. (Alguém aí sussurrou ‘quebra de simetria’? :mrgreen: ) Mais ainda, a função β é dada pela equação que define o fluxo de Ricci,

\beta(t) = \displaystyle\frac{\partial}{\partial t} g(t)= -2\,\mbox{Ric}(t) \; .

(A prova disso fica para o leitor interessado… mas também pode ser encontrada nas referências abaixo. 😉 )

O entendimento de como as soluções do fluxo de Ricci se comportam quando elas se aproximam um regime singular (i.e., quando elas vão chegando perto duma singularidade) é um passo chave para o uso do fluxo de Ricci (e.g., na prova da conjectura da geometrização). Mais ainda, de acordo com o que vimos na análise do fluxo do grupo de renormalização para modelos σ não-lineares, fica claro que nesse cenário também a formação de singularidades tem um papel fundamental — nesse caso, as soluções relevantes do fluxo de Ricci são as chamadas “ancient solutions”, aquelas que existem durante um intervalo máximo [de tempo], e correspondem a teorias renormalizáveis.

Uma classificação natural das singularidades pode ser feita com base na duração da existência de sua solução para o fluxo de Ricci e como essa solução escala assintoticamente. É possível também se usar técnicas de Convergência de Gromov-Hausdorff, em particular “point picking“.

Fica claro que o estudo da formação de singularidades é um dos tópicos principais na teoria de fluxos de Ricci, dado que ele provê o entendimento da estrutura das soluções em regimes de alta curvatura — em particular, a análise do “limite de colapso” do fluxo de Ricci é extremamente interessante: o colapso toma a forma duma simetria (“collapsing symmetry”) sob a qual o limite do fluxo de Ricci é eqüivariante (ver também Sistemas Dinâmicos Eqüivariantes, Eqüivariância e Cohomologia Eqüivariante). Esse é o fenômeno análogo à geração duma QFT a partir da quebra espontânea duma simetria. (Sem entrar em detalhes, sob a ação dessa “simetria de colapso”, as soluções limite do fluxo de Ricci passam a ter a estrutura dum Grupóide Riemanniano. 😛 Essa é uma noção familiar na teoria de foliações e no estudo de álgebras C* duma foliação — o que torna tudo ainda mais claro quando lembramos que cada solução duma dada QFT vive em sua própria folha e tem sua própria [representação] da álgebra C* em questão.) Portanto, há grande potencial e relevância em se usar esse tipo de técnica para se estudar o regime UV do grupo de renormalização em QFT.

Referências…

Enquete…

Júbilo…

Diversão garantida… 😈

Categorias:arXiv, hep-th, math-ph, Mathematics, Physics, Science Tags:, , , , , , , ,
  1. Rafael S. Calsaverini
    sábado, 21 fev 2009; \08\America/New_York\America/New_York\k 08 às 17:07:10 EST
    Responder

    Daniel,
    queria só confirmar uma questão de notação, para eu que sou um quase analfabeto mas to querendo ler seu post com cuidado.

    O que você chama de Map(S,M) é o conjunto das funções que levam elementos de S em elementos de M?

    E Act(U) é o conjunto das funções que levam U nos reais?

    Portanto Act[Map(S,M)xC] é o conjunto de funcionais que levam funções f:S->M (com parâmetros no conjunto C) nos reais? É isso?

    • Daniel
      sábado, 21 fev 2009; \08\America/New_York\America/New_York\k 08 às 17:26:22 EST
      Responder

      Rafa,

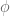      Exato, \mbox{Map}(\Sigma,\mathscr{M}) = \{\phi\,:\; \Sigma\rightarrow\mathscr{M}\}, i.e., é o conjunto das funções/mapas \phi que têm domínio em \Sigma e imagem em \mathscr{M}.

      Vc está correto quanto ao espaço das Ações também (com respeito a ambas as perguntas). 😉

      Será que isso ajuda? Vc viu algum erro que precisa ser corrigido, alguma imprecisão?

      []’s.

      • Rafael S. Calsaverini
        sábado, 21 fev 2009; \08\America/New_York\America/New_York\k 08 às 22:03:15 EST
        Responder

        Não, não… eu é que não estou acostumado com a notação.

        Estou tentando mentalmente traduzir para pedestres como eu no assunto.

  2. Leonardo
    sábado, 14 mar 2009; \11\America/New_York\America/New_York\k 11 às 09:48:52 EDT
    Responder

    Oi

    Para aqueles menos versados em matemática como eu, como complemento deste post, há uma palestra bem acessível do Marcelo Viana (IMPA) sobre fluxos de Ricci e a conjectura de Poincaré:

    http://video.if.usp.br/coloquio/conjectura-de-poincar-geometria-para-entender-o-universo

    Na verdade a palestra é mais sobre o segundo tópico, fluxos de Ricci ele explica por alguns minutos em termos da analogia com equilibrio termodinâmico 🙂

  3. JEAN LAURO MULLER
    quarta-feira, 28 out 2009; \44\America/New_York\America/New_York\k 44 às 09:09:33 EDT
    Responder

    Poderia se estabelecer uma conexão que define o fluxo de ricci no universo de gödel ?
    como estabelecer essa relação ?
    quais suas implicações físicas ?

    Agradeço a ajuda.

    • Daniel
      quarta-feira, 28 out 2009; \44\America/New_York\America/New_York\k 44 às 15:00:39 EDT
      Responder

      @ Jean,

      A fórmula pro Fluxo de Ricci é imediata, basta vc escolher a métrica que vc deseja usar (uma vez que o Tensor de Ricci é derivado da métrica) e substituir na fórmula. Isso deve responder suas 2 primeiras perguntas.

      Quanto a última pergunta, i.e., a aplicação da técnica do Fluxo de Ricci à métrica de Gödel, eu, pessoalmente, não conheço nenhum trabalho que trate desse problema. Mas, em princípio, não é nenhum bixo-de-7-cabeças, é mais uma aplicação direta do que qualquer outra coisa.

      Espero que isso ajude.

  4. Claudia Franchi
    terça-feira, 20 dez 2011; \51\America/New_York\America/New_York\k 51 às 15:57:41 EST
    Responder

    Olá,
    Poderia por favor me enviar material em português? É muito difíil de encontrar.

    • Daniel
      segunda-feira, 26 dez 2011; \52\America/New_York\America/New_York\k 52 às 15:59:45 EST
      Responder

      Oi Cláudia,

      Infelizmente, eu não conheço nenhum material em português sobre esse assunto. De fato, o trabalho original a conter essas idéias é a tese de PhD de D. Friedan, referência de número 9 na última referência acima.

      Até onde eu sei, este é o primeiro texto a tratar desse assunto em português (pt_BR).

  1. domingo, 22 fev 2009; \08\America/New_York\America/New_York\k 08 às 12:53:12 EST
    Algumas coisas que a física pode dizer sobre o Mercado Financeiro (Parte 1) « Ars Physica
  2. quarta-feira, 11 mar 2009; \11\America/New_York\America/New_York\k 11 às 17:43:45 EDT
    Teorias de Gauge: passado e futuro… « Ars Physica

Deixe um comentário