Giroscópio (Física Divertida)
Inspirado em uma das brilhantes e divertidíssimas aulas do Prof. Walter Levin, que você pode assistir em vídeos disponibilizados pelo MIT, no site do MITOCW, baixar no iTunes, ou mesmo assistir no youtube; falarei de um divertido “brinquedo”, que na verdade possui inúmeras aplicações, tendo como original aplicação o auxílio em navegações (veja mais sobre giroscópios aqui).
Abaixo a aula do Prof. Levin disponibilizada no youtube
A parte da aula na qual o tema giroscópio é abordado começa em 14:40 (eu recomendo assistir a aula inteira, excelente!). Note que quando o eixo da roda segurada em mãos é mudado, imediatamente surge uma força de oposição, tornando difícil continuar a girar o eixo da roda (sistema).
Abaixo um vídeo rápido que ilustra o experimento apresentado na video aula anterior (os vídeos não são relacionados):
Primeiramente lembremos o que seria o produto vetorial. Quando fazemos o produto vetorial entre dois vetores e
obtemos um terceiro vetor
perpendicular aos dois vetores anteriores. O módulo desse vetor é dado por
Onde A e B são os módulos dos vetores e
, e
o ângulo entre esses vetores. Antes de começarmos a discutir o modelo para o experimento mostrado nos vídeos anteriores, falaremos de torque. No dia-a-dia aplicamos torques em diversas ocasiões, quando abrimos uma porta, quando subimos em uma escada apoiada em uma parede, quando usamos uma chave-de-fenda para desparafusar alguma coisa, etc. Podemos dizer que o torque mede a tendência de colocarmos objetos a girar, quando aplicamos uma força
em um determinado ponto, à uma distância r (chamada braço) de um ponto de referência, de modo que o módulo do torque seja dado por

Torque causado por uma força F. Repare que a intensidade do torque depende do "braço de momento", e do ângulo entre este e a força aplicada. O módulo do torque também depende do ângulo formado entre estes dois vetores, sendo máximo quando a força aplicada for perpendicular ao braço.
Precisamos também de outro vetor importante, também um momento, que é associado à rotação, o chamado momento angular, esse vetor será especialmente difícil de justificar sem conceitos aprendidos no ensino superior, mas podemos tentar justificar de maneira razoável, o que seria fisicamente esse vetor.
O grande conflito é deixar de lado a concepção de que velocidade angular é um escalar, como apontado na grande maioria dos livros de ensino médio, na verdade é um vetor sempre perpendiular à velocidade tangencial e ao raio, como pode ser visto na figura abaixo.
O momento angular é uma grandeza importante, ainda mais quando ela for conservada (de maneira análoga ao momento linear), de forma que possamos explorar as simetrias do problema. A definição do momento angular é dada por
Onde é o momento de inércia e
é a velocidade angular. Vale ressaltar que que para um sistema de muitas partículas pontuais, o momento angular total é igual à soma dos momentos angulares de cada partícula constituinte do sistema analisado. Outra maneira de representar o momento angular é da seguinte maneira
Onde é o momento linear, e
é a distância do momento à origem. Agora podemos começar a descrição do experimento realizado nos vídeos acima. Abaixo uma figura ilustrativa do problema.

A figura ilustra o modelo teórico para o experimento, uma roda de massa M, e raio R. O braço de tamanho r é fixado ao centro geométrico da roda (centro), e a roda é considerada homogênea, de modo que seu centro geométrico coincida com seu centro de massa.
A roda de massa M e raio R, é fixada ao braço de comprimento r, bem em seu centro. Consideramos a distribuição de massa do sistema como sendo homogênea, e desprezamos a massa do suporte no qual a roda é fixada, de maneira que o centro de massa do sistema coincide com o centro da roda.
As forças atuando no sistema quando a roda é colocada a girar com velocidade angular constante, são, seu peso atuando verticalmente, e que causa um torque, em relação ao ponto P, que faz com que a roda despenque, e o momento angular, perpendicular à roda, causada devido à rotação da mesma.
A primeira análise do sistema ilustrado pela figura acima deve causar espanto, pois a força peso aos olhos desatentos é a única atuando no sistema, de modo que seja impossível que a roda permaneça girando, entretanto, observamos que isso realmente acontece, nos experimentos mostrados nos vídeos, por quê?
A resposta vem abaixo, na verdade não existe força resultante na vertical, pois um torque atuando no ponto P, de mesma intensidade que o peso Mg da roda permite que ela permaneça girando sem despencar. Veja ilustração abaixo

Sistema em equilíbrio, a roda da bicicleta permanece girando sem despencar, pois um torque de mesma intensidade que a força peso Mg da roda é aplicada no ponto P, de modo que a resultante das forças seja nula no sistema na direção vertical.
Já demos uma motivação para um modelo no qual a roda possa permanecer girando sem despencar, mas e como explicar a rotação no plano horizontal (precessão)? Essa discussão não é tão simples, mas é muito interessante. O aluno interessado deve assistir à aula-video do Prof. Levin, onde poderá ver que a frequência de precessão é dada por
Analisando a equação acima, podemos perceber que quando o torque é aumentado a frequência de precessão aumenta, e se o momento angular aumentar a frequência de precessão diminui. O momento angular pode ser variado, se mudarmos a distribuição de massa do sistema, ou se mudarmos a velocidade angular (de giro) da roda. O período de precessão é dado pela seguinte relação, já conhecida pelos bons alunos de ensino médio
Eu não vou estragar o prazer de vocês interessados alunos de verem a brilhante discussão que o Prof. Walter Levin faz. Ele explica a precessão da roda, e as “forças que surgem” quando ele tenta segurar a roda, depois que ela é posta a girar e tem seu eixo levemente rotacionado. Já adianto que tem a ver com a conservação do momento angular, o sistema tem a tendência de permanecer girando, e quando rotacionamos seu eixo, essa tendência surge como uma força de oposição à que estamos fazendo.
Uma referência bibliográfica que recomendo a leitura é a do volume 1 de Feynman Lectures in Physics, seções 20-2 à 20-4. Na verdade recomendo ler os três volumes inteiros! 😉




Belo post! 🙂
Uma dúvida bestinha me surgiu rsrs. Sendo o momento de inércia [; \vec I ;] do post algo que mede a inércia rotacional do corpo, este não deveria ser um escalar?
Pesquisei um pouco e vi que o [; I ;], em casos simples, pode ser tratado como escalar porém sua forma genérica é tensorial! Como meu conhecimento sobre tensores é tão vasto quanto a frase “tensores são vetores com 4 dimensões” me abstenho de divagações ;-]
Voltando… Minha pergunta era:
– Neste caso, você realmente está tratando o momento de inércia como um vetor ou fora um engano?
Obrigado, até. 🙂
Não foi engano não…hehehehehe
O tensor de momento de inércia é uma formulação mais geral para a formulação desse tipo de problema. Quando você tem um sistema com uma distribuição não tão homogênea de inércia rotacional, por exemplo um pião que além de girar, ele também precessiona.
O que acontece quando você calcula uma integral de momento de inércia, na verdade você está calculando o momento de inércia em torno de um eixo, na verdade são 9 integrais que você deve calcular, e depois coloca tudo no tensor momento de inércia, que no caso é representado por uma matriz quadrada de ordem 3, simétrica e real. Tem um teorema chamado teorema espectral que diz que você encontra apenas auto-valores reais quando a matriz é desse tipo (tem algo mais geral, mas vou ficar por aqui), isso quer dizer fisicamente que quando você aplica a matriz em um vetor, e o resultado desse produto é um número multiplicando o mesmo vetor, você tem um auto-valor.
Dá pra explorar bastante todas essas sutilezas…
Você me deu idéia para um novo post! rsrsrsrsrs 😉
Faltou completar o raciocínio…rsrsrs
isso quer dizer fisicamente que quando você aplica a matriz em um vetor, e o resultado desse produto é um número multiplicando o mesmo vetor, você tem um auto-valor, na verdade você encontrou um eixo de simetria desse seu sistema girante.
Se sua matriz for diagonal, e os termos da diagonal forem diferentes, significa que você tem três vetores que formam a base dessa sua matriz, você tem 3 eixos distintos de rotação, ou seja, quando você observa o sistema girando, é algo bem simétrico, como nesse problema que eu mostrei da roda de bicicleta. Ele gira no plano xz em torno do eixo y, ou seja você tem Iyy, e precessiona no plano xy, em torno do eixo z, ou seja você tem Izz (instantâneamente), e nesse momento Ixx = 0.
Quando a roda vai girando, ela vai mudando o eixo de giro, e passa por exemplo a girar em torno de uma reta no plano xy, do tipo y = x, dai voce passa a ter
termos cruzados do tipo Ixy = Iyx, e depois ela passa a girar em torno do eixo x, dai você tem Iyy = 0 e aparece o Ixx.
@Guilherme: complementando o Osvaldo, essa matriz I que é o tensor de inércia. Um vetor em 4-dimensões é um tensor de posto 1, uma matriz é um tensor de posto 2, mas também há tensores de posto 3, 4, … N. Basicamente, um tensor é um conjunto de números que satisfazem regras de transformações lineares, igual como os vetores {a,b,c…} e as matrizes, {{a,b,c}, {d,e,f}, {g, h, i}}. Como momento de inércia é calculado em relação a um eixo, você tem, explicando em mais detalhes o primeiro comentário do Osvaldo:
1. I ao longo do eixo x, nas direções x,y e z (três números)
2. I ao longo do eixo y, …
3. I ao longo do eixo z, …
isso dá os 9 números que ele falou, que podem ser organizados numa matriz 3×3.
Esse sistema é, de fato, muito interessante. Note que nos vídeos o eixo sempre fica paralelo ao chão, isso é basicamente para tornar o problema mais fácil de ser resolvido. No entando, costuma-se resolver esse problema no caso geral em cursos de mecânica e a solução também é bem interessante, embora algebricamente intrincada.
Como recurso didático vale muito a pena também dar uma olhada no corpo rígido livre, sem ação de torques externos. Nesse caso há descrições geométricas que são muitos simples de entender: a construção de Lagrange e de Poinsot. Em ambas se consideram o elipsóide que é definido pelo momento de inércia (que é uma forma quadrática positiva), mas na construção de Lagrange se mostra o movimento que o vetor momento angular (visto no referencial não-inercial atrelado ao corpo) faz sobre o elipsóide; e na de Poinsot o movimento que o elipsóide faz em torno do momento angular (visto pelo referencial inercial externo ao corpo).
É algo muito visual, muito bonito e simples. E que, na minha opinião, elucida o que é o momento de inércia e a interpretação física dos eixos principais de inércia sobre os quais o Osvaldo falou. Você vê então que os eixos principais de inércia são as direções em que se momento angular estiver, as rotações serão “puras”, ie, em que um rotação em um eixo não vai misturar com movimentos em outros eixos. Existem diversos brinquedos que exploram essa mistura, sendo um dos mais famosos o Russian Rattleback… sempre quis ter um. 😛
Mas e daí, como considerar um corpo rígido sem torque quando sempre temos a gravidade fazendo torque? Aqui é que entre o argumento bonito… por simples análise dimensional, você pode ver que na rotação de um corpo rígido como esse dos vídeos, aumentar a velocidade angular por um fator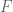 é equivalente a diminuir a gravidade por um fator
é equivalente a diminuir a gravidade por um fator  . Então, se você considerar um corpo que gira muito rápido ele fará um movimento que é essencial livre e descrito nas formas que falei acima – claro, isso só é interessante se agora você não começar mais paralelo ao chão. Essa idéia de passear pelo espaço de parâmetros de uma solução pode parecer simples, mas é amplamente utilizada: desde as teorias de escala em transições de fase até no estudo do grupo de renormalização de TQC.
. Então, se você considerar um corpo que gira muito rápido ele fará um movimento que é essencial livre e descrito nas formas que falei acima – claro, isso só é interessante se agora você não começar mais paralelo ao chão. Essa idéia de passear pelo espaço de parâmetros de uma solução pode parecer simples, mas é amplamente utilizada: desde as teorias de escala em transições de fase até no estudo do grupo de renormalização de TQC.
Acho que isso também responde um pouco a pergunta que o Leonardo se propôs num outro tópico. Quando um professor é defrontado com a pergunta “Para que serve a física?”, principalmente por alunos de ensino médio que aprendem modelos sobresimplificados e que naturalmente têm uma impressão da física ser algo completamente desconexo da realidade, eis a resposta: o estudo da física é um estudo de idéias! Mesmo que aquele modelo só seja capaz de descrever uma situação muito simplificada, a idéia de como descrevê-lo abre toda uma nova forma de pensar sobre a natureza.
Só uma última nota: eu concordo que a notação do produto entre o tensor de inércia e a velocidade angular ficou meio ambígua. Até porque o que você está fazendo não é um produto vetorial e sim um produto interno… eu acho que eu usaria .
.
Rafael,
Fiz a modificação que você sugeriu, obrigado! 😉
Obrigado pelos esclarecimentos rapazes e desculpa a demora para reply. O semestre começou e como vocês bem sabem o tempo contrai em vez de dilatar rsrs (sem graça essa, mais não resisti).
Até
Muito, Muito interessante.
Quero implementar um projeto de sistema com giroscopio/acelerometro em uma bicicleta com motor de 24/48 cc.
Inicialmente pensei em retirar destes helicopteros de baixo custo + os desafios de eletronica anologica digital e goolgando vi para estes mares bacanas.
Considerando que não tenho curso superior para compreender estas equações complexas, penso que ja valeu a pena o passeio por aqui pois ja estou atualizando minha agenda no google para os cursos do MIT e posteriormente focar onde tiver maior empatia.
Parabens pelo blog
Muito interessante e esclarecedor!
Parabéns pelo ótimo trabalho, me ajudou muito na compreensão sobre o assunto.